【108課綱】數學素養題 怎麼取材? 收藏
臺北市立麗山高中/黃靜寧老師 2019-12-30 108課綱 , 高中數學 , 新考招
1.佈題強調真實的情境與真實的問題。
2.評量的能力強調跨領域(學科)核心素養或是學科素養。
筆者連續兩年參與大考中心數學科素養試題研發計畫,過程中對素養試題的命題方向更趨於明確,故以下面例題嘗試說明試題設計的理念以供大家參考與指教。
素養導向試題舉例
命製試題時,最困難的部分就是試題的取材。試題的取材可以修自既有試題,亦可從周遭的生活情境中出發,以下將針對這兩部分舉例。(一)修自既有試題
【原試題】
箱中有編號分別為0,1,2,…,9的十顆球。隨機抽取一球,將球放回後,再隨機抽取一球。請問這兩球編號相減的絕對值為下列哪一個選項時,其出現的機率最大?
(1) 0 (2) 1 (3) 4 (4) 5 (5) 9 。
(出處:101年學測數學考科第6題)
※答案:2
【範例1】
摩天輪百貨公司周年慶為吸引顧客上門,提供消費者抽獎活動。周年慶期間,每天入館消費的前100 名民眾可參加百元禮券抽獎(禮券面額皆為100元),參加抽獎的民眾,從一個裝有分別標示1、2、…、9號共九顆球的箱子中抽出兩球,由抽出兩球的號碼差的數值可得到百元禮券的張數(例如:抽出兩球的號碼分別為2、6,則可得百元禮券四張)。試問:參加抽獎的民眾可獲得禮券金額的期望值是多少元。
(出處:台北區 1001-3-學測模擬考-數學考科)
※答案:1000/3
※說明:教學中所採用的例題多為號碼和,解法容易流於公式化,為評量學生能否將數學知識應用於解決問題,改採評量號碼差,引導學生應用有系統地計算原理,與當年學測欲評量的數學原理不謀而合。
※學習內容:將期望值應用於摸彩,求摸彩獎金的期望值。
(二)周遭中的生活情境
數學科的試題最常與生活情境結合的單元為機率與統計,如範例2以考生寫答試卷為情境評量機率概念。除此之外,其他章捷也有一些可評量數學概念應用在生活情境的試題,如範例3是以高速公路常見的交通號誌為評量情境三角比概念;範例4是科學新知所提之新制BMI為情境評量指數概念。範例3和範例4皆為大考中心試題研發小組所研發的試題。
【範例2】
※答案:(3)
※說明:考試是學生生活的重心,所以此題的內容可吸引學生注意,讓他們體會猜答做對的機率是很低的,而且此題的測驗目標還有評量學生的估算能力。
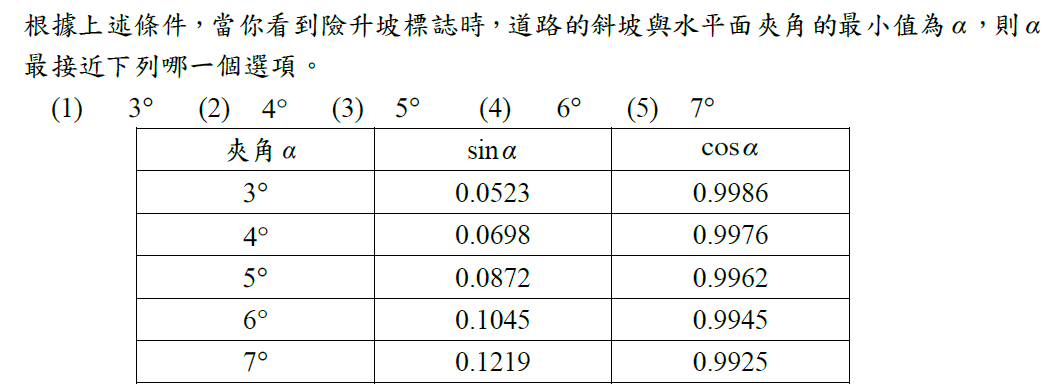
【範例3】
命題發想:下面的圖例是在高速公路常見的交通號誌,而這可評量高中數學什麼概念呢?經查險升坡與險降坡的定義後,於是有了下列的題組題。
※答案:(2)
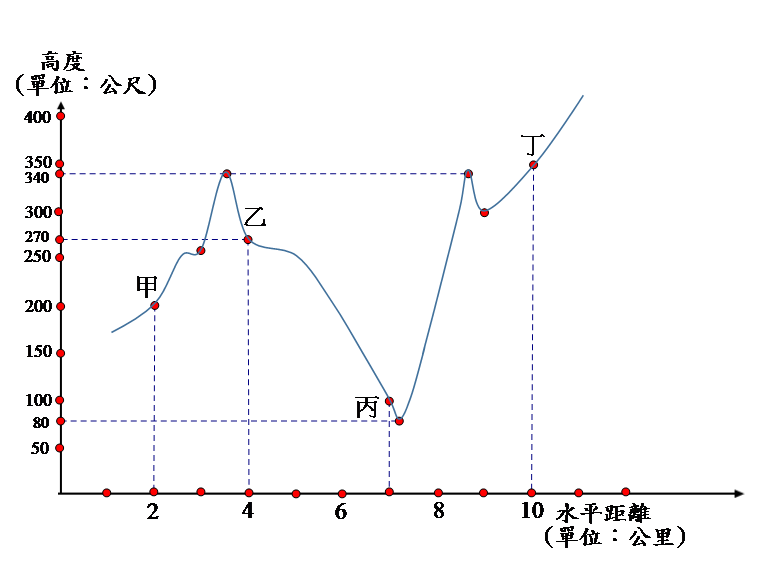
A-2:有一道路行經甲、乙、丙、丁四地,下圖為關於甲、乙、丙、丁四地的地形剖面圖,根據圖中的資料判斷坡度,選出正確選項。
(1) 由甲地到乙地路途中,不會看到險升坡號誌
(2) 由乙地到丙地路途中,會看到險降坡號誌
(3) 由丙地到丁地路途中,會看到險升坡號誌
(4) 由甲地到丁地全程中,會有在1公里的路程內先後看到險升坡與險降坡號誌
(5) 由甲地到丁地全程中,不會有坡度大於 10% 的路段
(出處:107年數學科研究測驗卷-卷二)
本試題為研究測試111年大學入學考試之用,仍須經評估與調整,尚非為大考中心正式考試之確定型式。
※答案:(2)(3)(4)
※說明:此題的構想源自平日在高速公路時,會看到一些交通號誌的招牌,進一步想了解號誌背後的限制,將坡度融入三角試題,培養學生平時便有觀察周遭環境的視野,甚至能將課堂的數學知識應用於其中。
※學習內容:將三角比的性質與地理科的地形剖面圖結合,應用於計算道路坡度,解決生活情境所遇到的問題。
【範例4】
英國牛津大學數學家尼克.崔佛生(Nick Trefethen)在2013年提出一項新制BMI計算方法,崔佛生指出,舊制BMI計算法純粹是以「體重(公斤)除以身高(公尺)的平方」,但卻忽略了高個子本身骨架較大,所以重量標準會更重的條件。因此,他所提出的新制BMI計算法,是「體重(公斤)先乘上1.3倍,再除以身高(公尺)的2.5次方」。現有甲、乙、丙三人的體重、身高如下表:
問三人中誰的新制BMI值會比舊制BMI值大?
(1) 甲 (2) 乙 (3) 丙 (4) 甲、乙 (5) 乙、丙 。
(出處:106年數學科研究測驗卷-卷五)
※答案:(1)
※說明:此題是比較兩種BMI計算公式的差別,生活中還有許多類似的公式存在,例如牛頓冷卻定律,同時兼具跨學科與生活情境應用。
※學習內容:利用指數的數學模型處理真實世界的問題(科學新知)。
※命題發想:科學知識不斷推陳出新,數學應用也要跟得上潮流,才能吸引學生的目光,提升學習興趣。
素養導向教學範例
考試引導教學,為了讓學生在面對素養試題能夠駕輕就熟,平日教學就應利用學生的生活環境中的實例。【教學範例】

上圖的相片是拍攝自公視門口的遮雨棚。由此遮雨棚出發,可引導學生探討的問題:
(1)定出遮雨棚三頂點在地面上投影點的坐標,利用平面向量求遮雨棚在地面上投影的面積。
(2)量出遮雨棚三頂點的高度,將三投影點的平面坐標轉換成遮雨棚三頂點的空間坐標,利用空間向量求遮雨棚的面積。
(3)利用遮雨棚三頂點的空間坐標,求出遮雨棚的所在的平面方程式。

結語
數學科素養試題的取材無所不在,為了讓學生能將數學知識融入生活的情境,平日教學就應透過生活實例,引導學生思考。當然素養試題如果能完全結合真實的生活的情境,當然是最理想的狀況;萬一無法呈現真實情境,老師也無須過於覺得挫敗,畢竟學生在過程中,領悟到解決問題的策略,日後遇到類似的情境,能夠將他在高中階段,所學習的方法,拿出來加以應用,對師生雙方而言,就算成功了。(本文反映專家作者意見,不代表本站立場)
★圖文由選才電子報同意授權轉載(節錄),原文請見:數學科素養試題的取材來源